Improving confidence in power spectra
Contents
Getting started
load SynthSig;
Intro
In the previous two tutorials we saw that there are some shortcomings to simply taking the raw powerspectra. First, if there is a large peak in the data it can leak energy to surrounding frequencies. Second, it is typically desirable to distinguish if a peak is significant. This typically requires some sort of averaging technique.
Reducing leakage.
The favoured method for reducing leakage is to window the data before performing the fft.
x = sig.x_peak; N = length(x); W = hanning(N)'; W = W./sqrt(mean(abs(W).^2)); y = x.*W; dt=median(diff(sig.t)); [px,f]=rawPowerSpec(x,dt); figure(2); clf subplot(2,1,1); plot(sig.t,x); hold on; ylabel('x [m]'); xlabel('t [s]'); subplot(2,1,2); loglog(f,px); hold on; set(gca,'ylim',[1e-6 1e3]); xlabel('F [Hz]'); ylabel('\phi_x [m^2 Hz^{-1}]'); print -dpng -r250 doc/NoWindow subplot(2,1,1); plot(sig.t,y,'b'); [py,f]=rawPowerSpec(y,dt); subplot(2,1,2); loglog(f,py,'b'); print -dpng -r250 doc/Window set(gca,'xlim',[0.2 0.8]); print -dpng -r250 doc/WindowZoom
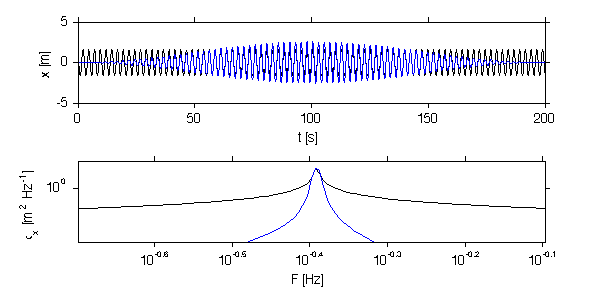
Here we see how applying the window has tightened the spectrum. Note however, that the peak has been spread a little bit into adjoining bins. Lets try on a braodband spectrum. Note that here we have to make the peak very prominent to make the effect important. However, also notice that the rest of the spectrum is not unduly disturbed.
figure(12);clf x = sig.x+30*sig.x_peak; W = hanning(N)'; W = N*W./sum(W); y = x.*W; clf subplot(3,1,1); plot(sig.t,x,sig.t,y); dt=median(diff(sig.t)); [px,f]=rawPowerSpec(x,dt); [py,f]=rawPowerSpec(y,dt); subplot(3,1,2); loglog(f,px,f,py); set(gca,'ylim',[1e-6 1e6]); xlabel('F [Hz]'); ylabel('\phi_x [m^2 Hz^{-1}]'); subplot(3,1,3); loglog(f,px,f,py); set(gca,'ylim',[1e-2 1e6]); xlabel('F [Hz]'); ylabel('\phi_x [m^2 Hz^{-1}]'); set(gca,'xlim',[1e-1 10e-1]); print -dpng -r250 doc/TaperingAgain

The Periodigram
The next procedure that is often carried out is to average the data somewhat. This can reveal shapes to the spectra that are not readily apparent in their rougher form.
The most common technique is the periodigram. This is accomplished by reshaping the data into blocks nfft long, windowing the data, and then taking the fft on each block. The resulting spectra are averaged. Because the windowing removes data at the edges, it is usual to overlap the windows by at least 50%. The overlapping logic requires a bit of care,
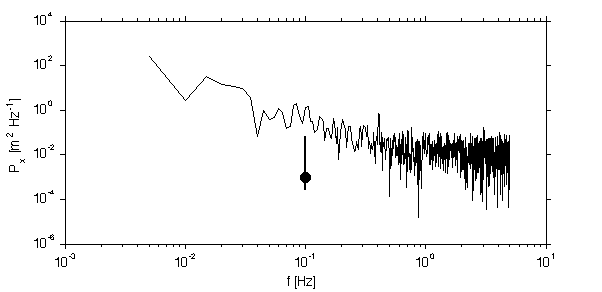
x = sig.x_r+sig.x_w+sig.x_peak/10; [px0,f0]=rawPowerSpec(detrend(x,0),dt); jmkfigure(11,2,0.4);clf [p,f,dof0,conf0]=periodogramPowerSpec(x,dt,length(x)); loglog(f,p); line([0.1 0.1],conf0/1000,'linesty','-','linewi',2) hold on;plot([0.1],1/1000,'o','markerfacecol','k','markersi',10) xlabel('f [Hz]'); ylabel('P_x [m^2 Hz^{-1}]'); if dop docprint('ConfInterval','FftTechniques.m'); end;
N =
2001
nind =
1
Spectral Smoothing...
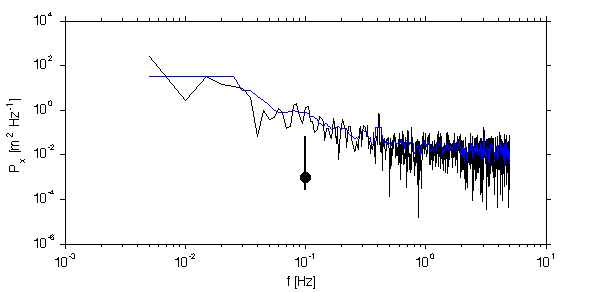
First, lets do the most obvious thing and smooth the spectra in frequency space...
psmooth = conv2(p,ones(1,10)/10,'same') loglog(f,psmooth,'b'); % set(gca,'xlim',[0.06 1]) line([0.1 0.1],conf0/1000,'linesty','-','linewi',2) if dop docprint('FreqSmooth','FftTechniques.m'); end;
psmooth =
Columns 1 through 8
32.1506 32.5134 32.5201 32.6132 32.6522 7.5511 7.3925 4.1905
Columns 9 through 16
2.7564 1.6744 0.9328 0.7766 0.8286 0.7602 0.8528 0.9494
Columns 17 through 24
0.8577 0.8117 0.8074 0.8021 0.6978 0.5343 0.5057 0.4851
Columns 25 through 32
0.3695 0.2425 0.2192 0.1943 0.2269 0.2426 0.1954 0.1699
Columns 33 through 40
0.1404 0.1463 0.1506 0.1726 0.1854 0.1949 0.1540 0.1317
Columns 41 through 48
0.1470 0.1479 0.1530 0.1461 0.1284 0.0928 0.0751 0.0643
Columns 49 through 56
0.0647 0.0594 0.0561 0.0566 0.0568 0.0560 0.0639 0.0827
Columns 57 through 64
0.0995 0.1122 0.1161 0.1227 0.1289 0.1119 0.1099 0.1094
Columns 65 through 72
0.1001 0.0831 0.0666 0.0534 0.0568 0.0501 0.0291 0.0299
Columns 73 through 80
0.0329 0.0340 0.0373 0.1031 0.1625 0.1646 0.1561 0.1641
Columns 81 through 88
0.1720 0.1694 0.1687 0.1681 0.1684 0.1048 0.0443 0.0394
Columns 89 through 96
0.0415 0.0369 0.0328 0.0379 0.0376 0.0360 0.0312 0.0298
Columns 97 through 104
0.0349 0.0350 0.0318 0.0291 0.0291 0.0257 0.0269 0.0351
Columns 105 through 112
0.0389 0.0415 0.0421 0.0421 0.0445 0.0431 0.0404 0.0405
Columns 113 through 120
0.0339 0.0286 0.0326 0.0354 0.0318 0.0311 0.0302 0.0339
Columns 121 through 128
0.0328 0.0335 0.0386 0.0462 0.0447 0.0358 0.0340 0.0351
Columns 129 through 136
0.0336 0.0301 0.0318 0.0352 0.0314 0.0203 0.0148 0.0178
Columns 137 through 144
0.0287 0.0382 0.0438 0.0459 0.0440 0.0381 0.0376 0.0386
Columns 145 through 152
0.0377 0.0347 0.0298 0.0362 0.0324 0.0349 0.0385 0.0387
Columns 153 through 160
0.0394 0.0391 0.0394 0.0398 0.0331 0.0169 0.0154 0.0133
Columns 161 through 168
0.0119 0.0120 0.0106 0.0139 0.0135 0.0176 0.0214 0.0244
Columns 169 through 176
0.0248 0.0213 0.0224 0.0260 0.0266 0.0245 0.0272 0.0226
Columns 177 through 184
0.0193 0.0156 0.0145 0.0146 0.0113 0.0094 0.0130 0.0160
Columns 185 through 192
0.0234 0.0283 0.0296 0.0313 0.0349 0.0394 0.0404 0.0400
Columns 193 through 200
0.0447 0.0417 0.0343 0.0326 0.0315 0.0307 0.0283 0.0249
Columns 201 through 208
0.0253 0.0282 0.0247 0.0261 0.0264 0.0268 0.0325 0.0409
Columns 209 through 216
0.0413 0.0405 0.0407 0.0379 0.0324 0.0304 0.0304 0.0273
Columns 217 through 224
0.0226 0.0138 0.0137 0.0163 0.0169 0.0151 0.0155 0.0183
Columns 225 through 232
0.0167 0.0179 0.0180 0.0192 0.0181 0.0168 0.0156 0.0193
Columns 233 through 240
0.0230 0.0213 0.0206 0.0191 0.0176 0.0171 0.0175 0.0163
Columns 241 through 248
0.0183 0.0175 0.0164 0.0151 0.0161 0.0185 0.0245 0.0347
Columns 249 through 256
0.0349 0.0360 0.0332 0.0315 0.0296 0.0293 0.0314 0.0320
Columns 257 through 264
0.0301 0.0275 0.0295 0.0291 0.0290 0.0295 0.0315 0.0330
Columns 265 through 272
0.0346 0.0378 0.0356 0.0275 0.0247 0.0240 0.0258 0.0250
Columns 273 through 280
0.0222 0.0205 0.0171 0.0114 0.0092 0.0104 0.0130 0.0153
Columns 281 through 288
0.0155 0.0155 0.0155 0.0178 0.0160 0.0170 0.0193 0.0191
Columns 289 through 296
0.0163 0.0168 0.0166 0.0162 0.0168 0.0163 0.0252 0.0340
Columns 297 through 304
0.0353 0.0361 0.0363 0.0335 0.0316 0.0315 0.0311 0.0313
Columns 305 through 312
0.0293 0.0209 0.0181 0.0177 0.0184 0.0186 0.0192 0.0229
Columns 313 through 320
0.0243 0.0240 0.0185 0.0179 0.0187 0.0195 0.0214 0.0233
Columns 321 through 328
0.0241 0.0216 0.0214 0.0197 0.0211 0.0221 0.0213 0.0207
Columns 329 through 336
0.0202 0.0190 0.0178 0.0191 0.0190 0.0204 0.0220 0.0236
Columns 337 through 344
0.0233 0.0250 0.0262 0.0260 0.0278 0.0306 0.0381 0.0402
Columns 345 through 352
0.0379 0.0341 0.0348 0.0338 0.0313 0.0306 0.0299 0.0246
Columns 353 through 360
0.0164 0.0157 0.0162 0.0172 0.0165 0.0140 0.0137 0.0154
Columns 361 through 368
0.0153 0.0147 0.0147 0.0154 0.0196 0.0224 0.0242 0.0256
Columns 369 through 376
0.0260 0.0256 0.0291 0.0325 0.0339 0.0337 0.0313 0.0289
Columns 377 through 384
0.0275 0.0271 0.0286 0.0339 0.0376 0.0352 0.0328 0.0287
Columns 385 through 392
0.0247 0.0237 0.0234 0.0224 0.0219 0.0196 0.0131 0.0137
Columns 393 through 400
0.0141 0.0142 0.0142 0.0138 0.0131 0.0130 0.0112 0.0105
Columns 401 through 408
0.0096 0.0109 0.0136 0.0155 0.0165 0.0171 0.0211 0.0221
Columns 409 through 416
0.0216 0.0180 0.0174 0.0145 0.0113 0.0097 0.0092 0.0091
Columns 417 through 424
0.0057 0.0046 0.0050 0.0110 0.0154 0.0153 0.0172 0.0193
Columns 425 through 432
0.0192 0.0192 0.0195 0.0195 0.0203 0.0157 0.0130 0.0142
Columns 433 through 440
0.0122 0.0108 0.0108 0.0108 0.0104 0.0104 0.0095 0.0080
Columns 441 through 448
0.0058 0.0051 0.0055 0.0048 0.0058 0.0083 0.0091 0.0103
Columns 449 through 456
0.0117 0.0120 0.0153 0.0172 0.0181 0.0188 0.0177 0.0164
Columns 457 through 464
0.0170 0.0156 0.0170 0.0177 0.0174 0.0179 0.0174 0.0165
Columns 465 through 472
0.0163 0.0154 0.0177 0.0266 0.0308 0.0349 0.0323 0.0310
Columns 473 through 480
0.0333 0.0335 0.0350 0.0359 0.0323 0.0239 0.0177 0.0151
Columns 481 through 488
0.0190 0.0240 0.0272 0.0279 0.0266 0.0247 0.0251 0.0269
Columns 489 through 496
0.0257 0.0240 0.0208 0.0147 0.0084 0.0075 0.0076 0.0084
Columns 497 through 504
0.0083 0.0081 0.0099 0.0103 0.0093 0.0096 0.0100 0.0136
Columns 505 through 512
0.0180 0.0198 0.0200 0.0183 0.0183 0.0224 0.0249 0.0250
Columns 513 through 520
0.0268 0.0254 0.0207 0.0182 0.0175 0.0169 0.0150 0.0099
Columns 521 through 528
0.0127 0.0179 0.0172 0.0162 0.0161 0.0175 0.0221 0.0251
Columns 529 through 536
0.0255 0.0314 0.0330 0.0280 0.0279 0.0271 0.0269 0.0256
Columns 537 through 544
0.0212 0.0193 0.0193 0.0159 0.0121 0.0121 0.0117 0.0127
Columns 545 through 552
0.0131 0.0131 0.0127 0.0123 0.0119 0.0101 0.0100 0.0111
Columns 553 through 560
0.0108 0.0093 0.0100 0.0139 0.0157 0.0154 0.0154 0.0151
Columns 561 through 568
0.0139 0.0162 0.0180 0.0182 0.0169 0.0139 0.0123 0.0138
Columns 569 through 576
0.0189 0.0229 0.0235 0.0225 0.0251 0.0300 0.0317 0.0312
Columns 577 through 584
0.0310 0.0300 0.0258 0.0216 0.0190 0.0157 0.0107 0.0066
Columns 585 through 592
0.0066 0.0102 0.0129 0.0122 0.0114 0.0116 0.0125 0.0144
Columns 593 through 600
0.0171 0.0168 0.0151 0.0112 0.0080 0.0080 0.0088 0.0104
Columns 601 through 608
0.0097 0.0079 0.0060 0.0141 0.0303 0.0408 0.0436 0.0458
Columns 609 through 616
0.0511 0.0529 0.0562 0.0589 0.0589 0.0512 0.0367 0.0270
Columns 617 through 624
0.0251 0.0232 0.0173 0.0142 0.0115 0.0113 0.0112 0.0109
Columns 625 through 632
0.0131 0.0126 0.0123 0.0122 0.0125 0.0123 0.0115 0.0089
Columns 633 through 640
0.0096 0.0109 0.0070 0.0076 0.0079 0.0075 0.0067 0.0076
Columns 641 through 648
0.0125 0.0160 0.0149 0.0125 0.0128 0.0128 0.0168 0.0200
Columns 649 through 656
0.0215 0.0230 0.0217 0.0197 0.0208 0.0215 0.0216 0.0217
Columns 657 through 664
0.0224 0.0196 0.0211 0.0190 0.0161 0.0147 0.0150 0.0142
Columns 665 through 672
0.0140 0.0129 0.0083 0.0082 0.0057 0.0052 0.0045 0.0049
Columns 673 through 680
0.0043 0.0097 0.0115 0.0116 0.0117 0.0117 0.0111 0.0111
Columns 681 through 688
0.0166 0.0201 0.0199 0.0152 0.0135 0.0146 0.0183 0.0215
Columns 689 through 696
0.0252 0.0271 0.0266 0.0234 0.0229 0.0242 0.0272 0.0283
Columns 697 through 704
0.0292 0.0299 0.0270 0.0249 0.0206 0.0229 0.0293 0.0320
Columns 705 through 712
0.0293 0.0295 0.0266 0.0233 0.0226 0.0239 0.0249 0.0264
Columns 713 through 720
0.0250 0.0211 0.0214 0.0218 0.0213 0.0218 0.0227 0.0245
Columns 721 through 728
0.0281 0.0264 0.0213 0.0213 0.0206 0.0183 0.0164 0.0175
Columns 729 through 736
0.0208 0.0228 0.0206 0.0184 0.0201 0.0224 0.0229 0.0222
Columns 737 through 744
0.0221 0.0197 0.0163 0.0109 0.0085 0.0086 0.0069 0.0043
Columns 745 through 752
0.0046 0.0056 0.0057 0.0057 0.0065 0.0101 0.0095 0.0087
Columns 753 through 760
0.0092 0.0099 0.0139 0.0188 0.0200 0.0202 0.0198 0.0178
Columns 761 through 768
0.0188 0.0199 0.0200 0.0190 0.0166 0.0116 0.0108 0.0115
Columns 769 through 776
0.0117 0.0103 0.0097 0.0095 0.0113 0.0126 0.0113 0.0117
Columns 777 through 784
0.0113 0.0110 0.0103 0.0123 0.0133 0.0122 0.0114 0.0102
Columns 785 through 792
0.0160 0.0188 0.0215 0.0241 0.0236 0.0214 0.0202 0.0213
Columns 793 through 800
0.0203 0.0201 0.0137 0.0098 0.0075 0.0062 0.0067 0.0075
Columns 801 through 808
0.0080 0.0072 0.0078 0.0100 0.0109 0.0113 0.0107 0.0098
Columns 809 through 816
0.0094 0.0110 0.0198 0.0260 0.0263 0.0256 0.0272 0.0280
Columns 817 through 824
0.0280 0.0286 0.0300 0.0278 0.0254 0.0267 0.0269 0.0266
Columns 825 through 832
0.0308 0.0333 0.0345 0.0356 0.0359 0.0370 0.0300 0.0228
Columns 833 through 840
0.0229 0.0222 0.0151 0.0114 0.0108 0.0117 0.0116 0.0110
Columns 841 through 848
0.0109 0.0120 0.0125 0.0134 0.0142 0.0142 0.0143 0.0130
Columns 849 through 856
0.0149 0.0163 0.0165 0.0176 0.0204 0.0227 0.0254 0.0259
Columns 857 through 864
0.0253 0.0232 0.0206 0.0226 0.0226 0.0223 0.0177 0.0138
Columns 865 through 872
0.0115 0.0143 0.0160 0.0169 0.0155 0.0135 0.0163 0.0157
Columns 873 through 880
0.0155 0.0188 0.0187 0.0156 0.0140 0.0142 0.0142 0.0123
Columns 881 through 888
0.0094 0.0077 0.0084 0.0054 0.0058 0.0064 0.0062 0.0061
Columns 889 through 896
0.0074 0.0075 0.0077 0.0082 0.0088 0.0141 0.0203 0.0259
Columns 897 through 904
0.0293 0.0298 0.0288 0.0287 0.0290 0.0290 0.0277 0.0220
Columns 905 through 912
0.0142 0.0077 0.0046 0.0035 0.0046 0.0052 0.0049 0.0046
Columns 913 through 920
0.0051 0.0097 0.0127 0.0148 0.0150 0.0151 0.0139 0.0156
Columns 921 through 928
0.0163 0.0172 0.0171 0.0128 0.0124 0.0164 0.0232 0.0274
Columns 929 through 936
0.0321 0.0321 0.0312 0.0325 0.0366 0.0377 0.0376 0.0342
Columns 937 through 944
0.0280 0.0235 0.0210 0.0222 0.0232 0.0209 0.0172 0.0160
Columns 945 through 952
0.0137 0.0108 0.0097 0.0103 0.0086 0.0072 0.0095 0.0119
Columns 953 through 960
0.0129 0.0148 0.0166 0.0181 0.0183 0.0194 0.0210 0.0201
Columns 961 through 968
0.0169 0.0146 0.0149 0.0168 0.0174 0.0168 0.0181 0.0182
Columns 969 through 976
0.0168 0.0161 0.0174 0.0184 0.0167 0.0137 0.0117 0.0109
Columns 977 through 984
0.0096 0.0081 0.0068 0.0070 0.0067 0.0064 0.0078 0.0070
Columns 985 through 992
0.0064 0.0062 0.0073 0.0071 0.0077 0.0073 0.0067 0.0060
Columns 993 through 1000
0.0043 0.0065 0.0140 0.0138 0.0122 0.0121 0.0115 0.0111
logarithmic smoothing...
loglog(f,logsmooth(p),'r'); if dop docprint('LogSmooth','FftTechniques.m'); end;

Periodigrams with incremental smoothing and confidence intervals...
Periodigram...
jmkfigure(12,2,0.8); clf subplot(3,1,1); loglog(f0,px0); hold on; % Theoretical power spectra % The three wave forms plotted above have known power spectra. f = f0; df = median(diff(f)); % it is usual to plot spectra in terms of cycles/s. P_w = f*0+var(sig.x_w)/max(f); P_r = f.^(-2); P_r = P_r./sum(P_r*df)*var(sig.x_r); P_peak = f*0; %in = find(om==om_peak); %P_peak(in) = 1*var(sig.x_peak)/df/10; % rename so we don't overwrite by accident. th.f=f; th.P_r=P_r; th.P_w=P_w; th.P_peak=P_peak; th.Px = th.P_r+th.P_w+th.P_peak; % loglog(th.f,th.P_w,'col',[1 1 1]*0.5); hold on; loglog(th.f,th.P_r,'r'); loglog(th.f,th.P_peak,'bx','markersi',10); loglog(th.f,th.Px,'k'); xlabel('f [Hz]'); ylabel('P_x [m^2 Hz^{-1}]'); title('Theoretical spectrum of synthetic signals'); set(gca,'ylim',[1e-2 5e2]); nfft_in = 512/2; N = length(x) nfft=min([nfft_in N]); repeats=round(2*N/nfft) starts = floor(linspace(1,N-nfft,repeats)) X = [1:nfft]'*ones(1,repeats); X = ceil(X+ones(nfft,1)*(starts-1)); t = sig.t; x0 = x;t0=t; x = x(floor(X)); t = t(floor(X)); % must remove the trend from each block x = detrend(x,0); W = hanning(nfft)'; W = sqrt(nfft)*W./norm(W); W = W./sqrt(mean(W.^2)); x = x.*repmat(W',1,size(x,2)); subplot(3,1,2); plot(t,x); hold on; plot(t0,x0+3); xlabel('t [s]'); ylabel('x [m]'); Px = dt*fft(x); dt = median(diff(sig.t)); N = nfft; if mod(N,2)==1 nn = nfft; else nn=nfft-1; end; f = (0:nfft-1)/nfft/dt; f = f(2:(nn/2)); Px = Px(2:(nn/2),:); Px =Px.*conj(Px)*2/dt/N; subplot(3,1,3); loglog(f,Px) hold on; loglog(f,nanmean(Px'),'linewi',2) loglog(th.f,th.Px,'linewi',1) set(gca,'ylim',[1e-2 1e2],'xlim',[1e-3 10]); xlabel('f [Hz]'); ylabel('P_x [m^2 Hz^{-1}]'); print -dpng -r200 doc/PeriodigramTech
N =
2001
repeats =
16
starts =
Columns 1 through 7
1 117 233 349 466 582 698
Columns 8 through 14
814 931 1047 1163 1279 1396 1512
Columns 15 through 16
1628 1745
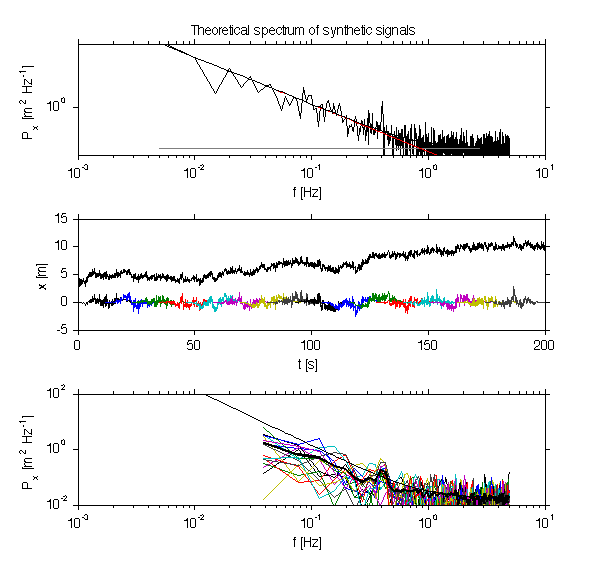
We can package th is procedure up into a periodigram m-file
Here we compare the results from 4 different fft lengths. The degrees of freedom and confidence intervals (in logarithmic space) are given. Note the peak only becomes statistically significant for nfft=512.
Also note the tradeoffs. The peak is less well resolved for shorter nfft. And less of the lower frequencies are resilved.
The other advantage, though, is a smoother resolution of the spectra at other frequencies. The take-home lesson is that a variety of spectral methods should be tried if the goal is data interpretation.
jmkfigure(3,2,0.5);clf
nfft = fliplr(256*[1 2 4 (length(x))/256]);
x = 2*sig.x_r+sig.x_w+sig.x_peak/10;
col ={'r','g','b','m'};
for i=1:length(nfft);
[p,f,dof(i),conf(i,:)]=periodogramPowerSpec(x,dt,nfft(i));
% [pp,ff]=pwelch(x,hanning(nfft(i)),nfft(i)/2,nfft(i),1/dt);
loglog(f,p,'col',col{i});
hold on;
loglog(th.f,th.Px,'col','k');
% loglog(ff,pp,':','col',col{i});
line([1 1]*10.^(i-4)*2,conf(i,:)*1e-4,'col',col{i},'linewi',2)
plot([1]*10.^(i-4)*2,1e-4,'o','markerfacecol',col{i},'col',col{i},'markersize',10)
text(10.^(i-4)*2,7e-6,sprintf('nfft=%d\ndof=%1.2f',nfft(i),dof(i)),'horizontalal','center');
hold on;
% loglog(ff,pp,'--','col',col{i});
set(gca,'ylim',[1e-6 1e2])
ppause
end;
xlabel('F [Hz]');
ylabel('\Phi_x [V^2 Hz^{-1}]');
if dop
print -dpng -r200 doc/Periodigrams
end;
ppause
if 1
i = 3
set(gca,'xlim',[0.1 1],'ylim',[0.01 10]);
line([1 1]*.6,conf(i,:)*1,'col',col{i},'linewi',2)
plot([1]*0.6,1,'o','markerfacecol',col{i},'col',col{i},'markersize',10)
print -dpng -r200 doc/PeriodigramsZoom
end;
N =
2001
starts =
Columns 1 through 7
1 125 250 374 499 623 748
Columns 8 through 14
873 997 1122 1246 1371 1495 1620
Column 15
1745
nind =
14.6328
Pausing...
N =
2001
starts =
1 489 977
nind =
2.9082
Pausing...
N =
2001
starts =
1 249 497 745 993 1241 1489
nind =
6.8164
Pausing...
N =
2001
starts =
Columns 1 through 7
1 125 250 374 499 623 748
Columns 8 through 14
873 997 1122 1246 1371 1495 1620
Column 15
1745
nind =
14.6328
Pausing...
Pausing...
i =
3

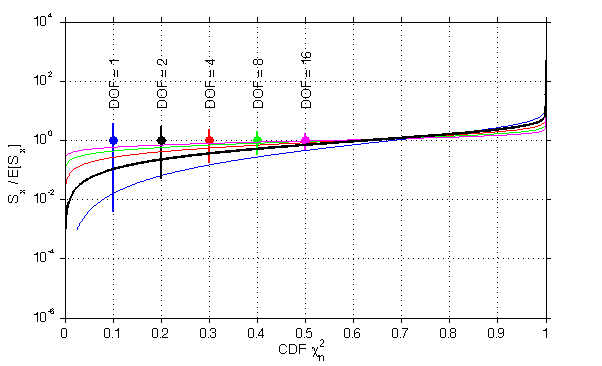
Plots of chi2 for these different degrees of freedom.
x = logspace(-3,3,1000);
jmkfigure(101,2,0.5);
clf
dof = [1 2 4 8 16];
nn = 0
col = {'b' 'k' 'r' 'g' 'm'}
for i=1:length(dof);
nn = nn+1;
pp = chi2cdf(x,dof(i));
semilogy(pp,x/dof(i),'col',col{i},'linewi',1);
hold on;
% set(gca,'xlim',[1e-2 100]);
grid on;
ind = find(pp>0.05);ind = ind(1);
ind2 = find(pp>0.95);ind2 = ind2(1);
line(nn*0.1*[1 1],[x(ind)/dof(i) x(ind2)/dof(i)],'linewi',2,'col',col{i});
plot(nn*0.1,1,'o','markersi',7,'markerfacecol',col{i},'linewi',2,'col',col{i});
text(nn*0.1,10,sprintf('DOF = %d',dof(i)),'rotat',90);
% line([0.01 100],[0.05 0.05]);
% line([0.01 100],1-[0.05 0.05]);
end;
pp = chi2cdf(x,2);
semilogx(pp,x/2,'linewi',2);
ylabel('S_x / E[S_x]','fontsi',12);
xlabel('CDF \chi^2_n','fontsi',12);
if dop
docprint('chi2','FftTechniques.m');
end;
% print -dpng -r150 doc/chi2
nn =
0
col =
'b' 'k' 'r' 'g' 'm'